BOJ-백준 4196번 도미노 C++ 문제 풀이 입니다.
링크 : https://www.acmicpc.net/problem/4196
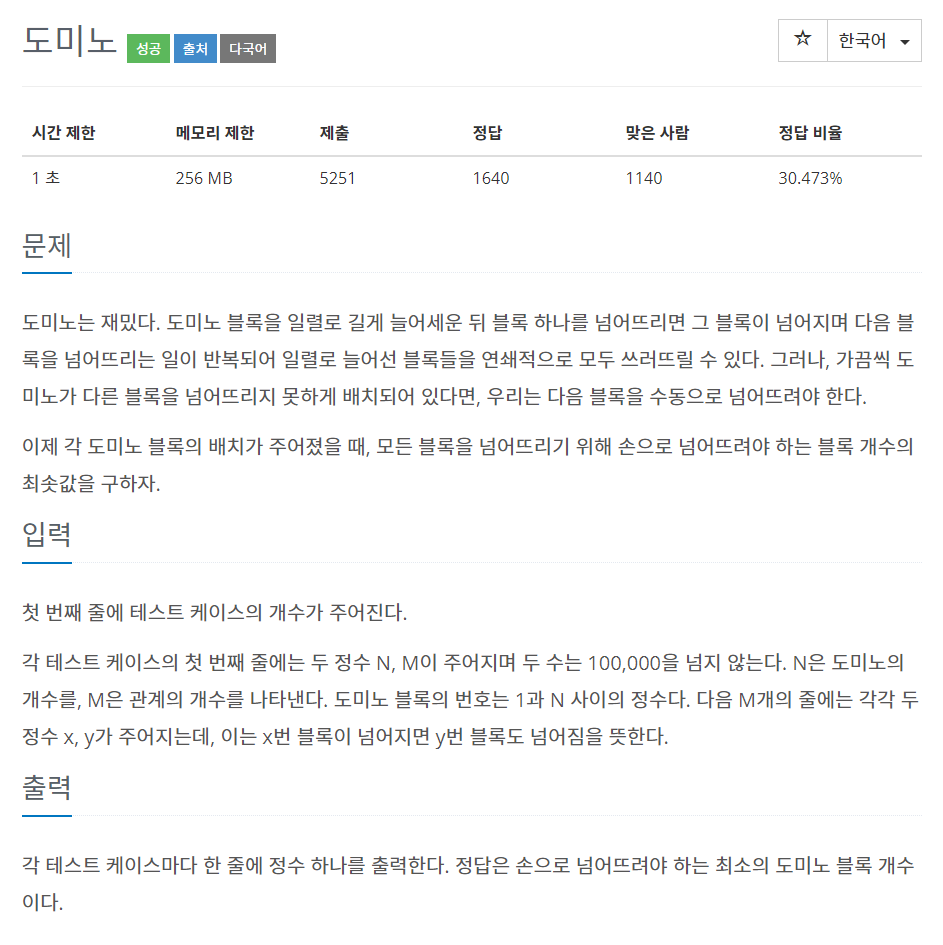
4196번: 도미노
도미노는 재밌다. 도미노 블록을 일렬로 길게 늘어세운 뒤 블록 하나를 넘어뜨리면 그 블록이 넘어지며 다음 블록을 넘어뜨리는 일이 반복되어 일렬로 늘어선 블록들을 연쇄적으로 모두 쓰러
www.acmicpc.net
✅ C++ 정답 코드 입니다. 더보기 클릭!
#include <iostream>
#include <vector>
#include <stack>
#define MAX 100001
using namespace std;
//n 도미노 총 개수, m 관계의 개수
int t,n,m;
int id, d[MAX];
bool finished[MAX];
vector<int> domino[MAX]; // 도미노 관계
vector<vector<int>> SCC; // 강한 결합요소
stack<int> s;
int group[MAX];
int inDegree[MAX];
int dfs(int x) {
// SCC를 생성을 수행하는 DFS
d[x] = ++id;
s.push(x);
int parent = d[x];
for(int i=0; i<domino[x].size(); i++){
int y =domino[x][i];
if(d[y] == 0) parent = min(parent, dfs(y));
else if(!finished[y]) parent = min(parent, d[y]);
}
if(parent == d[x]){
vector<int> scc;
while(1) {
int t = s.top();
s.pop();
scc.push_back(t);
group[t] = SCC.size()+1;
finished[t] = true;
if(t==x) break;
}
SCC.push_back(scc);
}
return parent;
}
void solve(){
scanf("%d %d", &n, &m);
//Init
SCC.clear();
fill(d, d+MAX, 0);
fill(inDegree,inDegree+MAX,0);
fill(finished, finished+MAX, 0);
for(int i=1; i<=n; i++){
domino[i].clear();
}
for(int i=0; i<m; i++){
int x, y;
scanf("%d %d", &x, &y);
domino[x].push_back(y);
} // 도미노 관계 그래프 만들기
for(int i=1; i<=n; i++){
if(d[i]==0) dfs(i);
}//SCC 그래프 만들기 완료
for(int i=1; i<= n; i++){
for(int j=0; j<domino[i].size(); j++){
int y = domino[i][j];
if(group[i] !=group[y])
++inDegree[group[y]];
}
}
int count = 0;
for(int i=1; i<=SCC.size(); i++){
if(inDegree[i]==0) count++;
}
printf("%d\n",count);
}
int main() {
cin >> t;
for(int tt=0; tt<t; tt++){
solve();
}
return 0;
}
📌 해설
SCC를 구하고 각 강한 결합 요소를 하나의 정점으로 간주합니다. 그리고 inDegree를 구해 inDegree가 0인 강한 결합 요소의 개수를 count하여 출력하면 정답을 받을 수 있습니다.
🚩 주의
테스트 케이스가 여러개 주어 질 수 있고, 도미노의 개수, 관계의 개수가 100,000 까지 입력될 수 있기 때문에 효율성에 유의합니다.
#include <iostream>
#include <vector>
#include <stack>
#define MAX 100001
using namespace std;
//n 도미노 총 개수, m 관계의 개수
int t,n,m;
int id, d[MAX];
bool finished[MAX];
vector<int> domino[MAX]; // 도미노 관계
vector<vector<int>> SCC; // 강한 결합요소
stack<int> s;
int group[MAX];
int inDegree[MAX];1. 필요한 변수를 모두 선언해 줍니다.
1-1. t 테스트 케이스 수, n 도미노 총 개수, m 관계의 개수
1-2. id 부모값을 초기화 하는 변수, d SCC 부모값을 저장하는 배열
1-3. finished SCC를 구할때 dfs가 끝난지 판별하는 배열
1-4. domino 도미노 관계 정보를 저장하는 변수
1-5. SCC 도미노의 SCC 관계를 저장하는 변수
1-6. s SCC를 구할때 필요한 스택 변수
1-7. group 각 도미도(노드)가 몇 번째 SCC에 속하는지 그룹으로 기록하는 배열
1-8. inDegree 각 SCC를 하나의 정점으로 간주하고 정점의 진입 차수를 기록하는 배열
int main() {
cin >> t;
for(int tt=0; tt<t; tt++){
solve();
}
return 0;
}1. main에서 테스트 케이스 수를 입력받고 테스트 케이스 만큼 solve() 함수를 호출합니다.
void solve(){
scanf("%d %d", &n, &m);
//Init
SCC.clear();
fill(d, d+MAX, 0);
fill(inDegree,inDegree+MAX,0);
fill(finished, finished+MAX, 0);
for(int i=1; i<=n; i++){
domino[i].clear();
}
for(int i=0; i<m; i++){
int x, y;
scanf("%d %d", &x, &y);
domino[x].push_back(y);
} // 도미노 관계 그래프 만들기
for(int i=1; i<=n; i++){
if(d[i]==0) dfs(i);
}//SCC 그래프 만들기 완료
for(int i=1; i<= n; i++){
for(int j=0; j<domino[i].size(); j++){
int y = domino[i][j];
if(group[i] !=group[y])
++inDegree[group[y]];
}
}
int count = 0;
for(int i=1; i<=SCC.size(); i++){
if(inDegree[i]==0) count++;
}
printf("%d\n",count);
}2. solve()
2-1. 입력을 받기 전 dfs에서 사용하는 변수들과 domino 벡터를 모두 비워줘서 초기화를 진행합니다.
2-2. 필요한 입력을 모두 받습니다.(도미노의 수, 관계의 수, domino 관계)
2-3. dfs를 수행하여 SCC 그래프를 완성합니다.
2-4. domino 정점을 모두 탐색하는 for문을 작성합니다.
2-4.(1) i 번 도미노에 연결된 도미노 번호를 y에 저장합니다.
2-4.(2) 만약, y번 도미노의 SCC와 i번 도미노의 SCC가 서로 다른 그룹에 속해 있다면 y의 그룹에서 i의 그룹으로 진입차수를 1 증가시킵니다.
2-5. 진입차수를 모두 구했으면, 각 SCC 그룹에서 진입 차수가 0인것을 count 하여 출력합니다.
int dfs(int x) {
// SCC를 생성을 수행하는 DFS
d[x] = ++id;
s.push(x);
int parent = d[x];
for(int i=0; i<domino[x].size(); i++){
int y =domino[x][i];
if(d[y] == 0) parent = min(parent, dfs(y));
else if(!finished[y]) parent = min(parent, d[y]);
}
if(parent == d[x]){
vector<int> scc;
while(1) {
int t = s.top();
s.pop();
scc.push_back(t);
group[t] = SCC.size()+1;
finished[t] = true;
if(t==x) break;
}
SCC.push_back(scc);
}
return parent;
}3. SCC를 생성하는 dfs
3-1. 부모값을 ++id로 초기화 합니다.
3-2. 자기자신(x)를 스택에 넣습니다.
3-3. parent 부모값을 d[x]값으로 선언하고 초기화 합니다.
3-4. 자신과 연결된 도미노를 탐색하는 for문을 작성합니다.
3-4.(1) 자신과 연결된 도미노의 번호를 y에 저장합니다.
3-4.(2) 만약 y번 도미노의 부모값이 단 한번도 초기화 되지 않았다면(방문된적이 없다면) 현재 부모값(parent)와 dfs(y)를 수행한 뒤 받은 부모값 중 더 작은 값을 parent에 저장합니다.
3-4.(3) 만약 y번 도미노가 방문된적이 있는데 아직 dfs가 끝나지 않은 도미노라면, 현재 부모값(parent)와 d배열에서 갱신된 y의 부모값 중 더 작은 값을 parent에 저장합니다.
3-5. 만약 현재 parent 값이 d배열에서 갱신된 부모값과 같다면 SCC를 생성합니다.
3-6. scc를 저장할 벡터를 선언합니다.
3-7. 스택의 top에서 원소(t)를 하나 꺼내 scc에 넣습니다.
3-8. group 배열에 t가 어느 SCC에 속하는지 기록합니다.
3-9. 스택의 원소를 모두 뺐다면 반복을 종료하고 scc를 SCC에 삽입합니다.
3-10. dfs는 parent를 반환하고 종료합니다.
::
오늘 하루 종일 이것만 풀었음..

'✅ 문제풀이' 카테고리의 다른 글
| BOJ-백준 9095번 1,2,3 더하기 C++ (0) | 2021.10.27 |
|---|---|
| BOJ-백준 3977번 축구 전술 C++ (0) | 2021.10.26 |
| BOJ-백준 2150번 SCC C++ (0) | 2021.10.25 |
| BOJ-백준 1671번 상어의 저녁식사 C++ (0) | 2021.10.24 |
| BOJ-백준 11377번 열혈강호3 C++ (0) | 2021.10.23 |



