BOJ-백준 11726번 2xn 타일링 C++ 문제 풀이 입니다.
링크 : https://www.acmicpc.net/problem/11726
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net

✅ C++ 정답 코드 입니다. 더보기 클릭!
#include <iostream>
using namespace std;
int t[1001];
int tile(int x) {
if(x==1) return t[x]=1;
if(x==2) return t[x]=2;
if(t[x]!=0) return t[x];
return t[x] = (tile(x-1) + tile(x-2))%10007;
}
int main() {
int n;
cin >> n;
int result = tile(n);
cout << result;
return 0;
}
📌 해설
다이나믹 프로그래밍 문제입니다. 타일을 붙이는 방법에 대한 점화식을 구하고 식을 구현하는 문제입니다. 출력에서 10007로 나눈 나머지를 구해야 하는데 이는 n이 조금만 커져도 출력해야하는 숫자가 엄청 커지기 때문에 오버플로우를 방지하고자 붙은 조건입니다.
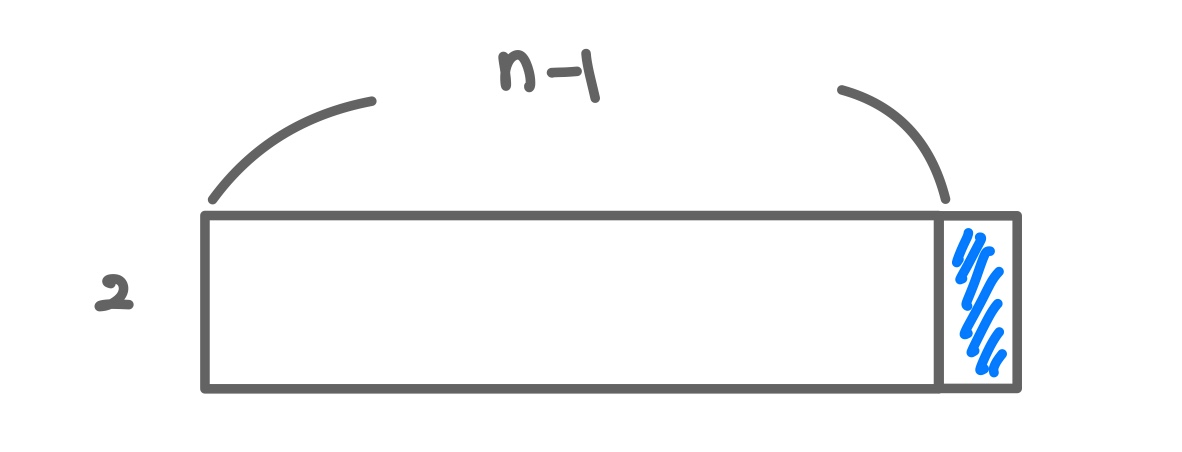
타일의 길이 n-1에서 n으로 1 증가하였다고 가정합니다.
이 때, 타일을 채울 때 세로로 긴 타일 하나를 붙이는 경우의 수만 가능합니다.

타일의 길이가 n-2에서 n으로 2 증가하였다고 가정합니다.
이때, 타일을 채울 때 가로로 긴 타일 두개를 붙이는 경우의 수만 가능합니다.
세로로 긴 두개의 타일을 붙이는 경우의 수는 이미 위(n-1)경우의 수 에 포함되어 있기 때문에 고려하지 않습니다.

따라서 길이가 n일때의 경우의 수는 n-1의 경우의 수와 n-2의 경우의 수를 더한 것과 같습니다.
즉, dp[n] = dp[n-1] + dp[n-2] 이라는 점화식을 세울 수 있습니다.
🚩 주의
n 이 1000까지 입력 될 수 있기 때문에 점화식 결과를 저장할 배열 변수는 1001개 선언해 줍니다.
오버플로우가 발생하지 않으려면 %10007은 return과 동시에 연산해줘야 합니다.
int tile(int x) {
if(x==1) return t[x]=1;
if(x==2) return t[x]=2;
if(t[x]!=0) return t[x];
return t[x] = (tile(x-1) + tile(x-2))%10007;
}1. 재귀 함수를 만듭니다.
재귀 종료조건을 명시하고( x==1, x==2) 만약 저장된 t가 없을 경우에만 재귀호출을 하여 값을 구합니다.
2. %10007 을 하고 t에 저장한 뒤 return합니다.
#include <iostream>
using namespace std;
int t[1001];
int main() {
int n;
cin >> n;
int result = tile(n);
cout << result;
return 0;
}3. main에서 n을 입력받은 뒤 결과를 result에 저장, 출력합니다.
::
DP 매우 어렵....!

'✅ 문제풀이' 카테고리의 다른 글
| BOJ-백준 2133번 타일 채우기 C++ (0) | 2021.10.18 |
|---|---|
| BOJ-백준 11727번 2xn 타일링 2 C++ (0) | 2021.10.17 |
| BOJ-백준 1748번 수 이어 쓰기 1 Python (0) | 2021.10.16 |
| BOJ-백준 6064번 카잉 달력 Python (0) | 2021.10.16 |
| BOJ-백준 10989번 수 정렬하기 3 (0) | 2021.10.15 |



