BOJ-백준 2133번 타일 채우기 C++ 문제 풀이 입니다.
링크 : https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
✅ C++ 정답 코드 입니다. 더보기 클릭!
#include <iostream>
using namespace std;
int dp[30];
int cal(int x){
if (x%2==1) return 0;
if (x==0) return dp[x]=1;
if (x==2) return dp[x]=3;
if (x==4) return dp[x]=11;
if (dp[x]!=0) return dp[x];
int result_dp = 3*cal(x-2);
for (int i=4; i <=x; i++){
result_dp += 2*cal(x-i);
}
return dp[x] = result_dp;
}
int main() {
int n;
cin >> n;
if (n%2==1){
cout << 0 ;
}else {
cout << cal(n);
}
}
📌 해설
다이나믹 프로그래밍 문제입니다. 다만, 점화식을 세울때 유의해야 할 부분이 몇가지 있는 문제였습니다.
우선, 벽이 3*n이기 때문에 홀수 n이 입력되는 경우 벽의 크기는(3,9,15,21,27...) 무조건 홀수로 떨어지므로 짝수 크기를 갖는 1*2, 2*1 타일로 벽을 모두 채울 수 없습니다.
즉, 홀수 입력이 주어진다면 채울 방법의 경우의 수가 없으므로 0을 출력합니다.

이제 점화식을 구하기 위해 n-2 길이가 주어진 뒤, 2가 증가한 상태의 3*n짜리 벽이 주어졌다고 생각해봅시다.
이 벽에서 늘어난 부분(3*2)을 채우기 위한 경우의 수를 구해본다면,

이렇게 3가지가 있습니다.
여기까지만 보면 점화식이 dp[n] = 3*dp[n-2] 인것 같지만 그렇지 않습니다.
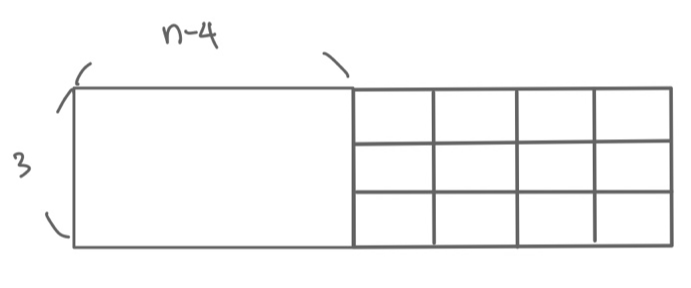
n-4 에서 4만큼 늘어난 n짜리 벽입니다. 늘어난 부분(3*4칸)부분을 채우는 경우의 수가 위(3*2칸)경우의 수를 제외한 경우의 수가 존재한다면 점화식이 달라집니다.

핑크색으로 체크가 되어있는 부분은 3*2칸의 경우의 수에 포함되는 부분이고 3*4칸에만 존재하는 경우의 수가 2가지 존재합니다. 여기까지 dp[n] = 3*dp[n-2] + 2*dp[n-4] 로 세울 수 있습니다.
n-6, n-8, ... 0 까지 n-2를 제외한 모든 n-짝수에는 경우의 수가 2가지 존재하므로 모든 경우의 수를 포함시켜 주어야 합니다.
따라서 점화식은 dp[n] = 3*dp[n-2] + 2*dp[n-4] + 2*dp[n-6] + ... + 2*dp[0] 입니다.
🚩 주의
홀수 입력은 0을 출력할 수 있도록 합니다.
int cal(int x){
if (x%2==1) return 0;
if (x==0) return dp[x]=1;
if (x==2) return dp[x]=3;
if (x==4) return dp[x]=11;
if (dp[x]!=0) return dp[x];
int result_dp = 3*cal(x-2);
for (int i=4; i <=x; i++){
result_dp += 2*cal(x-i);
}
return dp[x] = result_dp;
}1. 종료 조건을 만듭니다.
만약 홀수가 입력되면 0을 반환하고 종료합니다.
dp[0]은 1을 반환하고 종료합니다.
dp[2]는 3을 반환하고 종료합니다.
만약 dp에 값이 없다면(0) result_dp를 계산합니다.
계수가 3인 dp[x-2]를 먼저 result_dp에 저장한 뒤
for 반복문을 통해 계수가 2인 나머지들을 모두 result_dp에 합산합니다.
for문이 종료되고 dp[x]를 반환합니다.
int main() {
int n;
cin >> n;
if (n%2==1){
cout << 0 ;
}else {
cout << cal(n);
}
}2. main에서는 n 을 입력받고
입력된 n이 홀수면 0을 출력, 짝수면 경우의 수를 계산하는 함수를 호출하고 결과를 출력합니다.
::
재귀호출 너무 어려운거 아닌가요...?

'✅ 문제풀이' 카테고리의 다른 글
| BOJ-백준 2252번 줄 세우기 C++ (0) | 2021.10.21 |
|---|---|
| BOJ-백준 14852번 타일 채우기 3 C++ (0) | 2021.10.18 |
| BOJ-백준 11727번 2xn 타일링 2 C++ (0) | 2021.10.17 |
| BOJ-백준 11726번 2xn 타일링 C++ (0) | 2021.10.17 |
| BOJ-백준 1748번 수 이어 쓰기 1 Python (0) | 2021.10.16 |



